Two-dimensional coordinate system
The modern Cartesian coordinate system in two dimensions (also called a
rectangular coordinate system) is commonly defined by two axes, at right angles
to each other, forming a plane (an xy-plane). The horizontal axis is labeled x,
and the vertical axis is labeled y. In a three-dimensional coordinate system,
another axis, normally labeled z, is added, providing a sense of a third
dimension of space measurement. The axes are commonly defined as mutually
orthogonal to each other (each at a right angle to the other). All
the points in a Cartesian coordinate system taken together form a so-called Cartesian plane.
The point of intersection, where the axes meet, is called the origin normally
labeled O. With the origin labeled O, we can name the x-axis Ox and the y-axis
Oy. The x and y axes define a plane that can be referred to as the xy-plane.
Given each axis, choose a unit length, and mark off each unit along the axis,
forming a grid. To specify a particular point on a two dimensional coordinate
system, you indicate the x unit first (abscissa), followed by the y unit
(ordinate) in the form (x,y), an ordered pair. In three dimensions, a third z unit (applicate) is added, (x,y,z).
The choices of letters come from the original convention, which is to use the
latter part of the alphabet to indicate unknown values. The first part of the
alphabet was used to designate known values.
An example of a point P on the system is indicated in the picture below using
the coordinate (5,2).
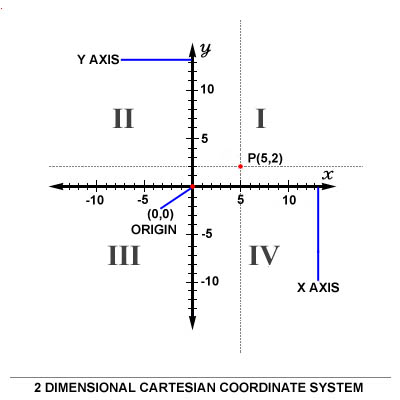
In the two-dimensional Cartesian coordinate system, a point P in the xy-plane
is represent by a tuple of two components (x,y).
- x is the signed distance from the y-axis to the point P,
and
- y is the signed distance from the x-axis to the point P.
In the three-dimensional Cartesian coordinate system, a point P in the
xyz-space is represent by a tuple of three components (x,y,z).
- x is the signed distance from the yz-plane to the point P,
- y is the signed distance from the xz-plane to the point P,
and
- z is the signed distance from the xy-plane to the point P.
The arrows on the axes indicate that they extend forever in the same
direction (i.e. infinitely). The intersection of the two x-y axes creates four
quadrants indicated by the Roman numerals I, II, III, and IV. Conventionally,
the quadrants are labeled counter-clockwise starting from the northeast
quadrant. In Quadrant I the values are (x,y), and II:(-x,y), III:(-x,-y) and
IV:(x,-y).
| Quadrant |
x values |
y values |
| I |
> 0 |
> 0 |
| II |
< 0 |
> 0 |
| III |
< 0 |
< 0 |
| IV |
> 0 |
< 0 |
See also