Vector
In physics and engineering, the word vector typically refers to a quantity
that has close relationship to the spatial coordinates, informally described as
an object with a "magnitude" and a "direction".
A common example of a vector is force � it has a magnitude and an orientation
in three dimensions (or however many spatial
dimensions one has), and multiple forces sum according to the parallelogram law.
Definitions
Informally, a vector is a quantity characterized by a number (indicating
magnitude) and a direction, often represented graphically by an arrow. Examples
are "moving north at 90 km/h" or "pulling towards the center of Earth with a
force of 70 newtons".
Examples of vectors include displacement, velocity, electric field, momentum,
force, and acceleration.
Vectors can be contrasted with scalar quantities such as distance, speed,
energy, time, temperature, charge, power, work, and mass, which have magnitude,
but no direction (they are invariant under coordinate rotations). The magnitude
of any vector is a scalar.
Representation of a vector
Symbols standing for vectors are usually printed in boldface as a. The
length or magnitude or norm of the vector
a is denoted by |a|.
Vectors are usually shown in graphs or other diagrams as arrows, as
illustrated below:
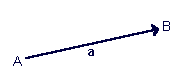
Here the point A is called the tail, base, start, or origin; point B is
called the head, tip, endpoint, or destination. The length of the arrow
represents the vector's magnitude, while the direction in which the arrow points
represents the vector's direction.
In order to calculate with vectors, the graphical representation is too
cumbersome. Vectors in a n-dimensional Euclidean space can be represented
as a linear combination of n mutually perpendicular unit vectors. Let's
consider R3 as an example. In R3,
we usually denote the unit vectors parallel to the x-, y- and z-axes
by i, j and k respectively. Any vector a in R3
can be written as a = a1i
+ a2j + a3k
with real numbers a1, a2
and a3 which are uniquely
determined by a. Sometimes a is then also written as a 3-by-1 or
1-by-3 matrix:
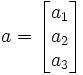
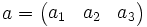
even though this notation suppresses the dependence of the coordinates a1,
a2 and a3
on the specific choice of coordinate system i, j and k.
See also